library(tidyverse)3 Medición endémica
Una endemia estará definida por la frecuencia de la enfermedad en un período de tiempo determinado; una vez alcanzado cierto umbral, la endemia pasa a ser epidemia.
3.1 Canal endémico
Para conocer la frecuencia regular de una enfermedad endémica y predecir su comportamiento, es necesario calcular el índice endémico y elaborar el canal endémico de la misma, los cuales permiten conocer las variaciones de dicha frecuencia en el tiempo.(Jaramillo Arango 2010)
3.1.1 Método de los cuartiles
Los cuartiles son los tres valores que dividen la distribución ordenada en cuatro partes con igual número de observaciones. (Blas 2007)
Aquí se presenta la descripción de los 3 cuartiles:
Cuartil 1 (Q1): Separa el 25% inferior de los valores ordenados, del 75% superior.
Cuartil 2 (Q2): Igual a la mediana; separa el 50% inferior de los valores ordenados, del 50% superior.
Cuartil 3 (Q3): Separa el 75% inferior de los valores ordenados, del 25% superior. (Triola 2004)
Vale la pena mencionar que los cuartiles son una medida de posición; por tanto, primero se debe calcular la posición del cuartil y luego buscar en los datos cuál es el valor que se encuentra en esa posición.

\[\begin{equation}{} Posición = Q\frac{n+1}{4} \end{equation}\]
Donde:
Q = Número de cuartil (1, 2 o 3).
n = Número total de datos.
Cada cuartil representa una parte del canal endémico:
- Q1 = Piso endémico.
- Q2 = Índice endémico.
- Q3 = Techo endémico.
Los cuartiles a su vez delimitan las distintas zonas del canal y los niveles de endemia:
Menor a Q1 = Zona de éxito (hipoendemia).
Entre Q1 y Q2 = Zona de seguridad (mesoendemia).
Mayor a Q2 y menor o igual a Q3 = Zona de alarma (hiperendemia).
Mayor a Q3 = Zona de epidemia.
Los pasos para realizar el canal endémico mediante el método de los cuartiles es el siguiente:
Paso 1. Ordenar los datos de menor a mayor.
Paso 2. Calcular la posición de cada cuartil.
Paso 3: Buscamos los valores correspondientes a cada posición obtenida.
Paso 4: Graficamos.
Dependiendo del software utilizado los valores de los cuartiles de un mismo conjunto de datos pueden variar. En R hay 9 métodos distintos para calcular los cuartiles, por defecto R utiliza el método 7, mientras que la fórmula aquí presentada se corresponde al método 6; sin embargo, la función quantile nos permite especificar el método mediante el comando type.
A continuación se muestra la comparación entre el método 7 (usado en R por defecto) y el método 6 (mostrado en la fórmula de arriba, especialmente práctico si se hace el cálculo manual).
ejemplo_datos_cuartiles <- c(1,2,3,4,5,6,7)
# Método 7
quantile(ejemplo_datos_cuartiles) 0% 25% 50% 75% 100%
1.0 2.5 4.0 5.5 7.0 # Método 6
quantile(ejemplo_datos_cuartiles, type = 6) 0% 25% 50% 75% 100%
1 2 4 6 7 Ahora veamos un ejemplo completo de la realización del canal endémico:
Usaremos los datos de PPC en México de 1995 a 1999 presentados por (Jaramillo Arango 2010) y con ellos crearemos un data.frame.
ppc_mexico <-
data.frame(
año = rep(1995:1999, each = 12),
mes = factor(rep(c(1:12), 5)),
casos = c(0, 0, 0, 0, 0, 1, 0, 2, 0, 2, 2, 1,
2, 1, 2, 0, 0, 2, 2, 5, 3, 4, 1, 2,
3, 9, 11, 19, 16, 15, 9, 19, 20, 14, 11, 4,
8, 15, 4, 5, 8, 6, 7, 9, 8, 11, 6, 20,
3, 5, 13, 2, 7, 1, 0, 7, 1, 4, 0, 0))Calculamos los coeficientes requerios (Piso, Índice y Techo):
canal_endemico_ppc <- ppc_mexico |>
group_by(mes) |>
summarise(Piso_endémico = quantile(casos, 0.25, type = 6),
Techo_endémico = quantile(casos, 0.75, type = 6),
Índice_endémico = quantile(casos, 0.5, type = 6)
) Procedemos a graficar mediante una gráfica de líneas.
ggplot(canal_endemico_ppc) +
geom_point(aes(mes,Piso_endémico), col = "green") +
geom_point(aes(mes,Techo_endémico), col = "red") +
geom_point(aes(mes, Índice_endémico), col = "blue") +
geom_line(aes(mes,Piso_endémico), col = "green", group = 1) +
geom_line(aes(mes,Techo_endémico), col = "red", group = 1) +
geom_line(aes(mes, Índice_endémico), col = "blue", group = 1) +
ylab("Casos") + xlab("Mes") +
ggtitle("Canal endémico", subtitle = "PPC México 1995-1999") +
theme_minimal()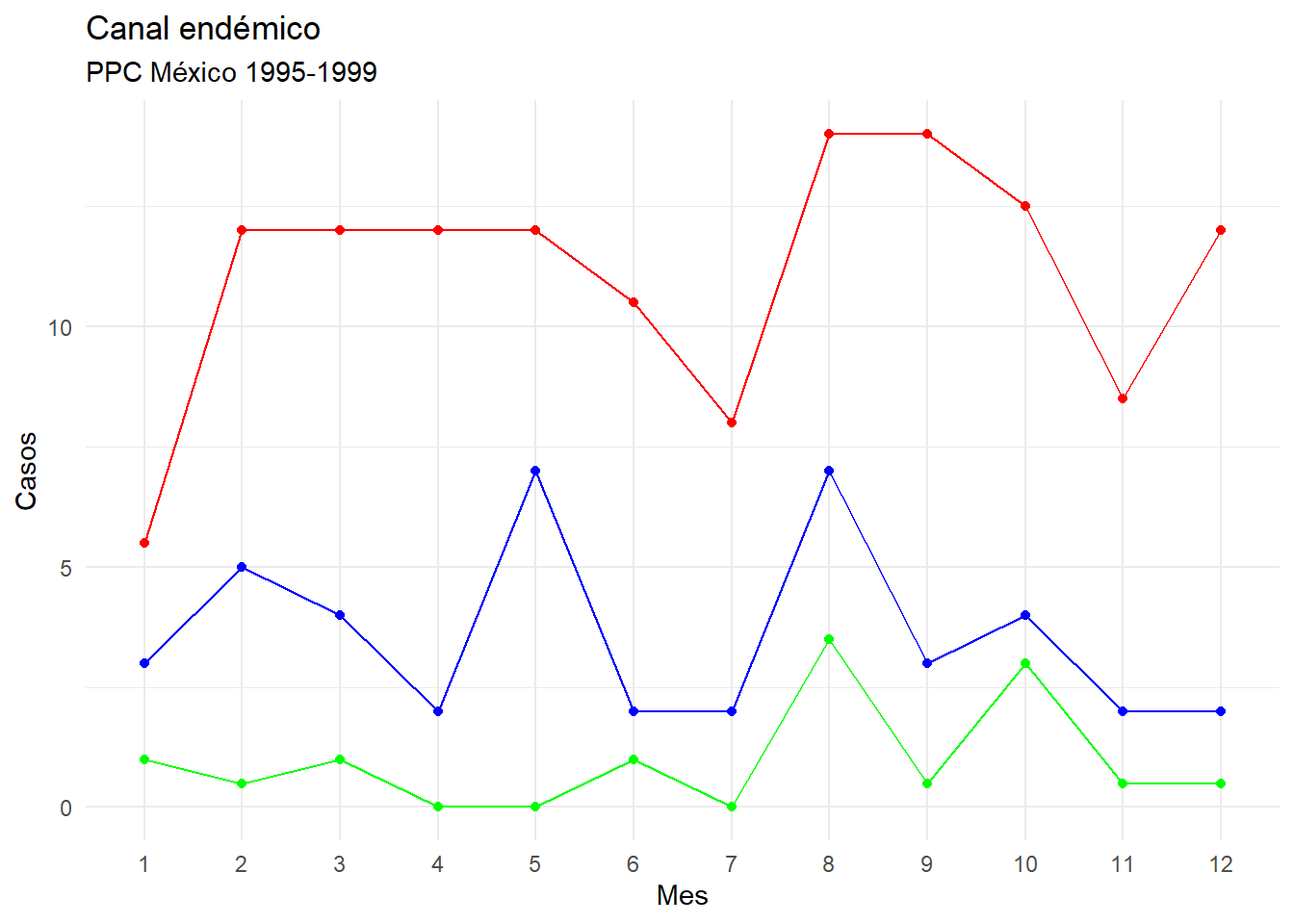
Podemos hacer también la gráfica con un manto de color para cada zona para mejorar la visualización.
ggplot(canal_endemico_ppc) +
geom_ribbon(aes(x = 1:12, xmin = 1,
ymin = 0, ymax = 15), fill = "green") +
geom_ribbon(aes(x = 1:12, xmin = 1,
ymin = Piso_endémico, ymax = 15), fill = "blue") +
geom_ribbon(aes(x = 1:12, xmin = 1,
ymin = Índice_endémico, ymax = 15), fill = "yellow") +
geom_ribbon(aes(x = 1:12, xmin = 1,
ymin = Techo_endémico, ymax = 15), fill = "red") +
xlab("Mes") + ylab("Casos") +ggtitle("Canal endémico PPC", subtitle = "México 1995-1999") +
scale_x_continuous(breaks = seq(0,12, 1)) +
scale_y_continuous(breaks = seq(0, 15, 1)) +
theme_classic() +
annotate(geom = "text",
x = 2,
y = min(canal_endemico_ppc$Piso_endémico),
label = "Éxito") +
annotate(geom = "text",
x = 2,
y = min(canal_endemico_ppc$Índice_endémico),
label = "Zona segura") +
annotate(geom = "text",
x = 2,
y = min(canal_endemico_ppc$Techo_endémico),
label = "Zona de alarma") +
annotate(geom = "text",
x = 2,
y = max(canal_endemico_ppc$Techo_endémico),
label = "Epidemia")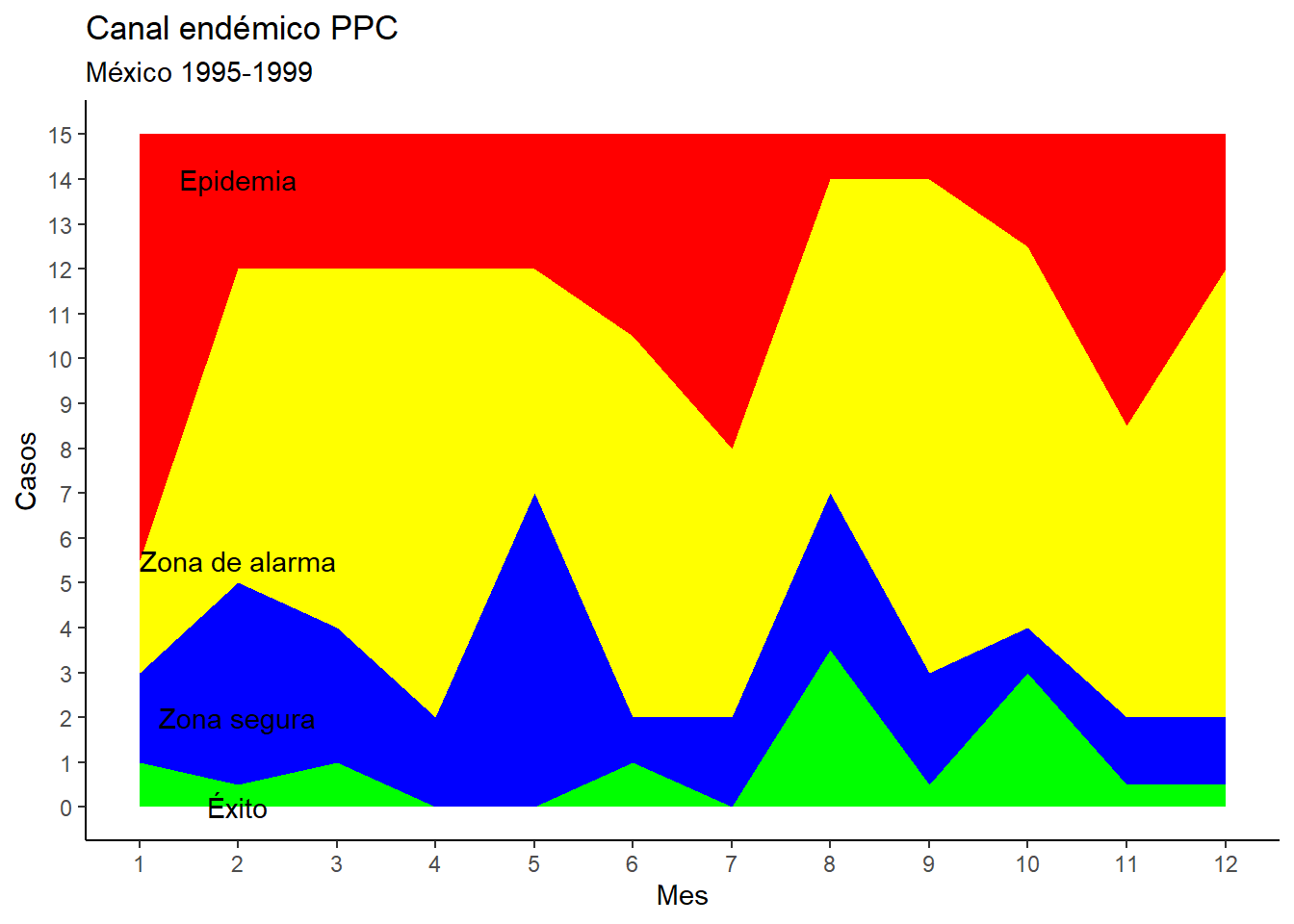
# ggplot(canal_endemico_ppc) +
# geom_line(aes(mes,Piso_endémico), fil = "black", group = 1, size = 1) +
# geom_line(aes(mes,Techo_endémico), col = "black", group = 1, size = 2) +
# geom_line(aes(mes, Índice_endémico), col = "black", group = 1, size = 2) +
# geom_ribbon(aes(x = 1:12, xmin = 1,
# ymin = 0, ymax = 15), fill = "green", alpha = 0.3) +
# geom_ribbon(aes(x = 1:12, xmin = 1,
# ymin = Piso_endémico, ymax = 15), fill = "blue", alpha = 0.3) +
# geom_ribbon(aes(x = 1:12, xmin = 1,
# ymin = Índice_endémico, ymax = 15), fill = "yellow", alpha = 0.3) +
# geom_ribbon(aes(x = 1:12, xmin = 1,
# ymin = Techo_endémico, ymax = 15), fill = "red", alpha = 0.3) +
# xlab("Mes") + ylab("Casos") +ggtitle("Canal endémico PPC", subtitle = "México 1995-1999") + theme_minimal()3.1.2 Canal endémico y boxplot
Hay una relación entre el canal endémico calculado mediante el método de los cuartiles y los boxplot (también llamados gráficas de cajas y bigotes).
La relación está en que un boxplot representa precisamente los cuartiles de un conjunto de datos.
Veámoslo con un ejemplo:
Tenemos un conjunto de datos que se presenta a continuación
ejemplo_datos_box_plot <- c(1,2,3,4,5,6,7)
ejemplo_datos_box_plot[1] 1 2 3 4 5 6 7Podemos hacer un resumen de estos datos con el comando summary.
summary(ejemplo_datos_box_plot) Min. 1st Qu. Median Mean 3rd Qu. Max.
1.0 2.5 4.0 4.0 5.5 7.0 Min. = Mínimo, representa el menor valor presente en el conjunto de datos que no supere el límite inferior
1st Qu. = Primer cuartil
Median = Segundo cuartil
Mean = Promedio.
3rd Qu. = Tercer cuartil
Max. = Máximo, representa el mayor valor presente en el conjunto de datos que no supere el límite superior
Estos datos que obtuvimos con summary son los que se representan en un boxplot (a excepción del promedio), veámolo a continuación:
boxplot(ejemplo_datos_box_plot)
text(x = 0.6, y = 1, "Mínimo")
text(x = 0.6, y = 2.5, "Q1")
text(x = 0.6, y = 4, "Q2")
text(x = 0.6, y = 5.5, "Q3")
text(x = 0.6, y = 7, "Máximo")
arrows(x0 = 0.65, x1 = 0.78, y0 = 1, y1 = 1)
arrows(x0 = 0.65, x1 = 0.78, y0 = 2.5, y1 = 2.5)
arrows(x0 = 0.65, x1 = 0.78, y0 = 4, y1 = 4)
arrows(x0 = 0.65, x1 = 0.78, y0 = 5.5, y1 = 5.5)
arrows(x0 = 0.65, x1 = 0.78, y0 = 7, y1 = 7)
arrows(x0 = 1.22, x1 = 1.3, y0 = 2.5, angle = 0)
arrows(x0 = 1.22, x1 = 1.3, y0 = 5.5, angle = 0)
arrows(x0 = 1.3, x1 = 1.3, y0 = 2.5, y1 = 5.5, angle = 0)
arrows(x0 = 1.3, x1 = 1.35, y0 = 4, y1 = 4)
text(x = 1.4, y = 4, "RIQ")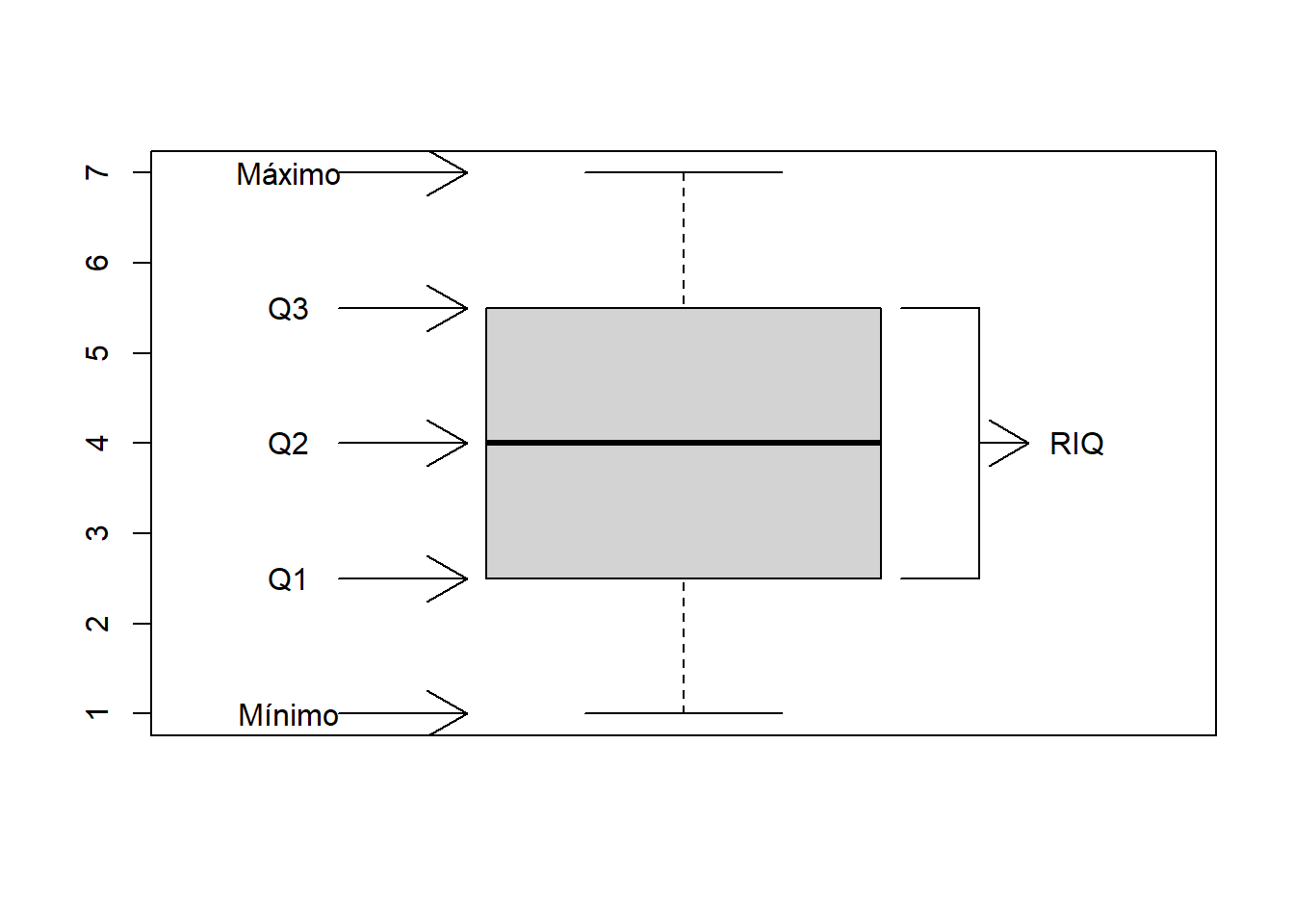
El RIQ (rango intercuartílico) es la diferencia entre el Q3 y el Q1.
A veces en la gráfica aparece algúno o varios círculos arriba del valor máximo y/o abajo del valor mínimo, estos son llamados valores atípicos o outliers, y son todos aquellos valores que se encuentren arriba del límite superior o abajo del límite inferior, siendo los límites calculados de la siguiente manera:
Límite superior (Ls) = Q3 + (1.5 * RIC).
Límite inferior (Li) = Q1 - (1.5 * RIC).
Veamos entonces el paralelismo del boxplot con el canal endémico
boxplot(ejemplo_datos_box_plot)
arrows(x0 = 0.65, x1 = 0.75, y0 = 2.5, y1 = 2.5, angle = 0)
arrows(x0 = 0.7, x1 = 0.7, y0 = 2.5, y1 = 1)
arrows(x0 = 0.65, x1 = 0.75, y0 = 5.5, y1 = 5.5, angle = 0)
arrows(x0 = 0.7, x1 = 0.7, y0 = 5.5, y1 = 7)
arrows(x0 = 0.7, x1 = 0.7, y0 = 2.5, y1 = 5.5, angle = 0)
arrows(x0 = 0.65, x1 = 0.75, y0 = 4, y1 = 4, angle = 0)
text(x = 0.65, y = 1.75, "Éxito")
text(x = 0.65, y = 3.25, "Seguridad")
text(x = 0.65, y = 4.75, "Alarma")
text(x = 0.65, y = 6.25, "Epidemia")
arrows(x0 = 1.25, x1 = 1.35, y0 = 2.5, y1 = 2.5, angle = 0)
arrows(x0 = 1.3, x1 = 1.3, y0 = 2.5, y1 = 1)
arrows(x0 = 1.25, x1 = 1.35, y0 = 5.5, y1 = 5.5, angle = 0)
arrows(x0 = 1.3, x1 = 1.3, y0 = 5.5, y1 = 7)
arrows(x0 = 1.3, x1 = 1.3, y0 = 2.5, y1 = 5.5, angle = 0)
arrows(x0 = 1.25, x1 = 1.35, y0 = 4, y1 = 4, angle = 0)
text(x = 1.3, y = 1.75, "Hipoendemia")
text(x = 1.3, y = 3.25, "Mesoendemia")
text(x = 1.3, y = 4.75, "Hiperendemia")
text(x = 1.3, y = 6.25, "Epidemia")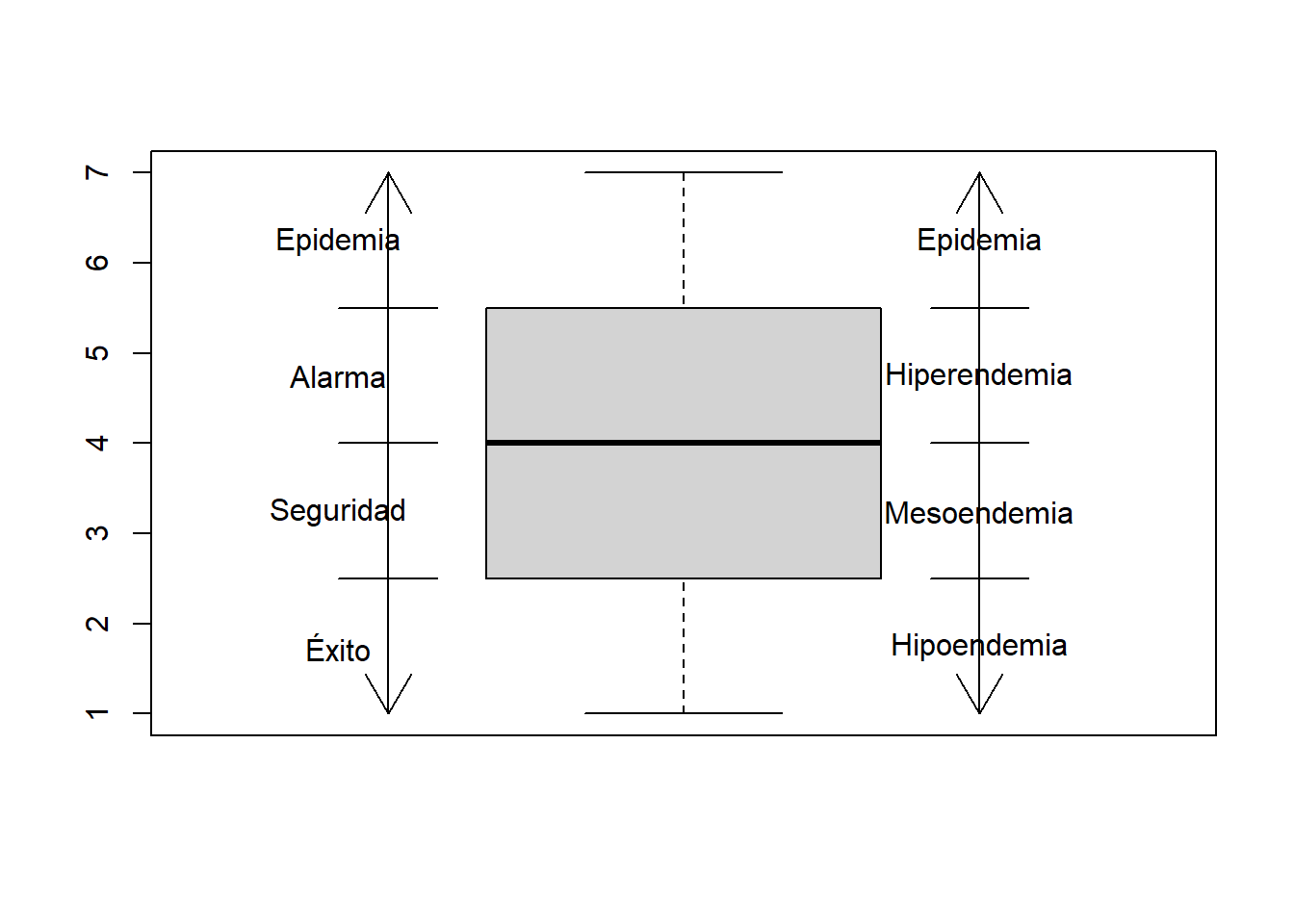
Graficación del canal endémico con boxplot (usaremos el ejemplo de ppc en México de 1995 a 1999 ya utilizado antes):
# Datos a usar
ppc_mexico <-
data.frame(
año = rep(1995:1999, each = 12),
mes = factor(rep(c(1:12), 5)),
casos = c(0, 0, 0, 0, 0, 1, 0, 2, 0, 2, 2, 1,
2, 1, 2, 0, 0, 2, 2, 5, 3, 4, 1, 2,
3, 9, 11, 19, 16, 15, 9, 19, 20, 14, 11, 4,
8, 15, 4, 5, 8, 6, 7, 9, 8, 11, 6, 20,
3, 5, 13, 2, 7, 1, 0, 7, 1, 4, 0, 0))- Boxplot con cuartiles calculados mediante el método 7 (por defecto en R)
ggplot(ppc_mexico, aes(mes, casos)) +
geom_boxplot()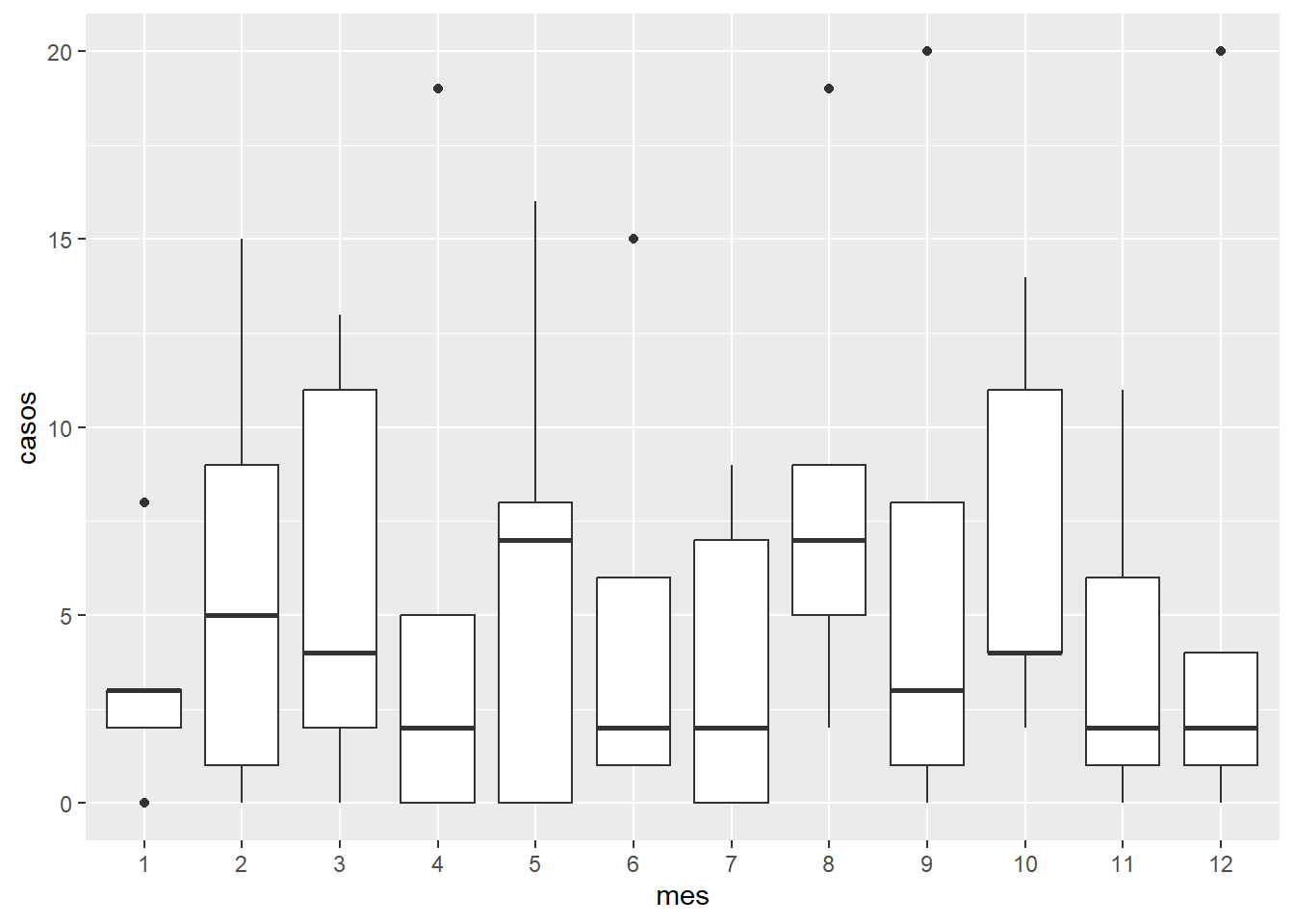
- Boxplot con cuartiles calculados mediante el método 6.
Cálculo de los coeficientes del canal endémico
canal_endemico_ppc <- ppc_mexico |>
group_by(mes) |>
summarise(Piso_endémico = quantile(casos, 0.25, type = 6),
Techo_endémico = quantile(casos, 0.75, type = 6),
Índice_endémico = quantile(casos, 0.5, type = 6)
) Graficación del canal endémico en forma de boxplot
ggplot(canal_endemico_ppc, aes(mes)) +
geom_boxplot(
aes(ymin = Piso_endémico,
lower = Piso_endémico,
middle = Índice_endémico,
upper = Techo_endémico,
ymax = Techo_endémico),
stat = "identity"
) +
theme_classic()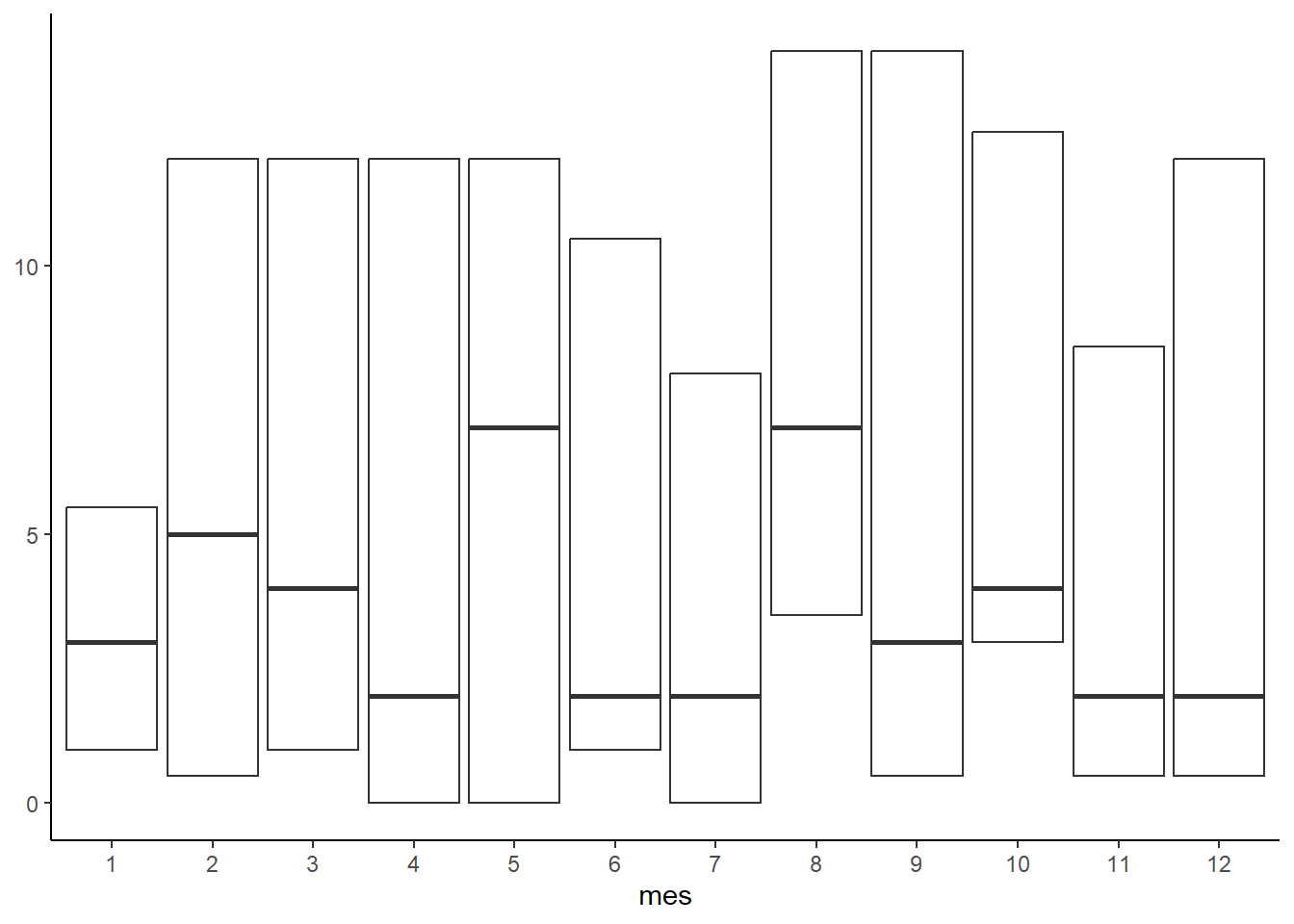
Ahora se mostrará la gráfica clásica de líneas sobre el boxplot para observar de manera más clara la relación entre el canal endémico mediante el método de los cuartiles y las gráficas de cajas.
ggplot(canal_endemico_ppc, aes(mes)) +
geom_boxplot(
aes(ymin = Piso_endémico,
lower = Piso_endémico,
middle = Índice_endémico,
upper = Techo_endémico,
ymax = Techo_endémico),
stat = "identity"
) +
geom_point(aes(mes,Piso_endémico), col = "green") +
geom_point(aes(mes,Techo_endémico), col = "red") +
geom_point(aes(mes, Índice_endémico), col = "blue") +
geom_line(aes(mes,Piso_endémico), col = "green", group = 1) +
geom_line(aes(mes,Techo_endémico), col = "red", group = 1) +
geom_line(aes(mes, Índice_endémico), col = "blue", group = 1) +
theme_minimal()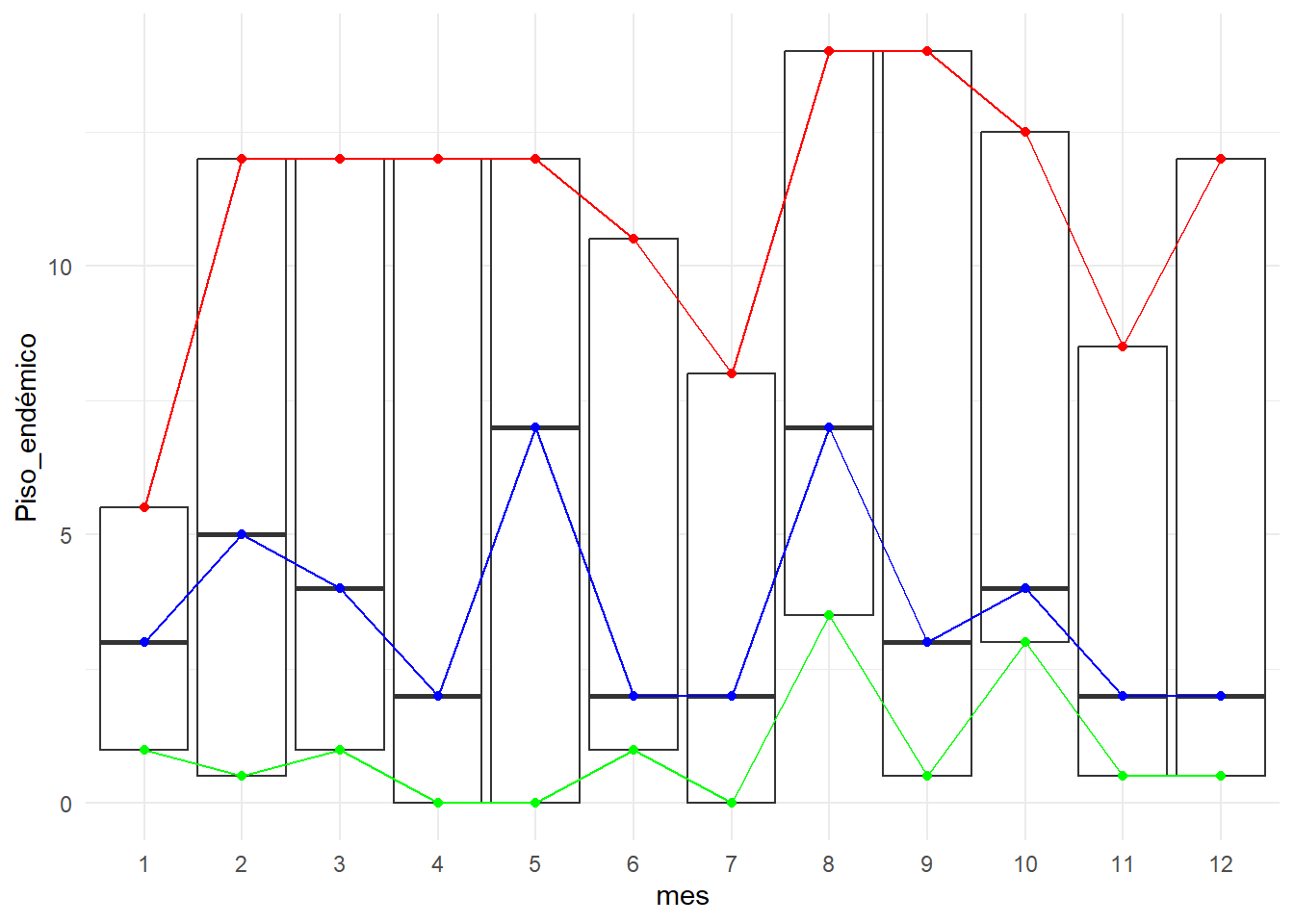
Ahora se mostrará la gráfica sombreada sobre el boxplot para terminar de comprender la relación.
ggplot(canal_endemico_ppc, aes(mes)) +
geom_boxplot(
aes(ymin = Piso_endémico,
lower = Piso_endémico,
middle = Índice_endémico,
upper = Techo_endémico,
ymax = Techo_endémico),
stat = "identity"
) +
geom_ribbon(aes(x = 1:12, xmin = 1,
ymin = 0, ymax = 15), fill = "green", alpha = 0.25) +
geom_ribbon(aes(x = 1:12, xmin = 1,
ymin = Piso_endémico, ymax = 15), fill = "blue", alpha = 0.25) +
geom_ribbon(aes(x = 1:12, xmin = 1,
ymin = Índice_endémico, ymax = 15), fill = "yellow", alpha = 0.25) +
geom_ribbon(aes(x = 1:12, xmin = 1,
ymin = Techo_endémico, ymax = 15), fill = "red", alpha = 0.25) +
theme_minimal()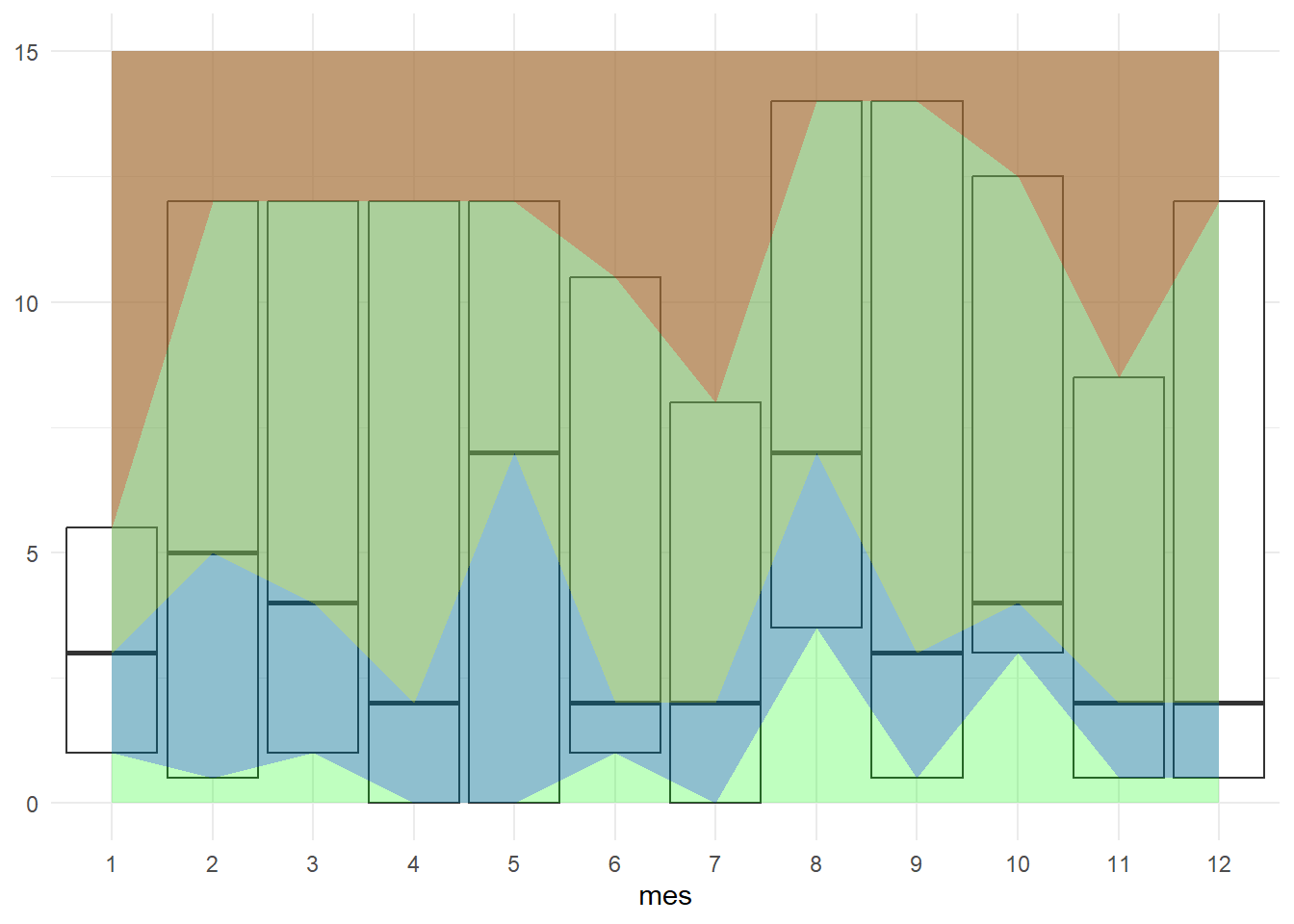
3.1.3 Evaluación de escenarios
Se presentan los casos reportados de Cisticercosis en Guatemala entre el año 2010 y 2014
cisticercosis_guate <- data.frame(
año = rep(2010:2014, each = 12),
mes = rep(1:12, 5),
casos = c(14, 16, 13, 14, 16, 15, 14, 16, 16, 16, 15, 16,
2, 5, 3, 9, 5, 7, 10, 2, 3, 5, 3, 4,
25, 22, 20, 20, 20, 18, 25, 18, 18, 17, 18, 18,
15, 14, 18, 17, 17, 17, 15, 13, 14, 15, 15, 14,
23, 24, 15, 22, 18, 20, 24, 19, 20, 19 , 22, 21)
)
#Primeros 6 registros
head(cisticercosis_guate) año mes casos
1 2010 1 14
2 2010 2 16
3 2010 3 13
4 2010 4 14
5 2010 5 16
6 2010 6 15Además, se presentan 3 escenarios hipotéticos para el año 2015
e1 <- data.frame(año = rep(2015, 12),
mes = 1:12,
casos = c(6, 8, 10,
9, 14, 13,
12, 13, 15,
19, 22, 21)
)
e2 <- data.frame(año = rep(2015, 12),
mes = 1:12,
casos = c(14, 13, 14,
12, 16, 15,
14, 15, 14,
15, 14, 14)
)
e3 <- data.frame(año = rep(2015, 12),
mes = 1:12,
casos = c(26, 28, 24, 23, 30, 32, 28, 30, 32, 28, 26, 27)
)Calcule la frecuencia de Éxito, Seguridad, Alarma y Epidemia de cada escenario
Ordene los escenarios de mejor a peor
Una forma que se nos puede ocurrir para determinar cuál es el mejor escenario es graficarlos juntos y ver cuál tiene los valores más bajos cada mes, a continuación se presenta esa gráfica comparativa
ggplot(e1) +
geom_line(aes(mes, casos), linetype = 1) +
geom_point(aes(mes, casos)) +
geom_line(aes(e2$mes, e2$casos), linetype = 2 ) +
geom_point(aes(e2$mes, e2$casos), shape = 15) +
geom_line(aes(e3$mes, e3$casos), linetype = 3) +
geom_point(aes(e3$mes, e3$casos), shape = "*", size = 4) +
scale_x_continuous(breaks= 1:12) +
annotate(geom = "text", x = 1, y = 35, label = "• E1") +
annotate(geom = "text", x = 1, y = 30, label = "■ E2") +
annotate(geom = "text", x = 1, y = 25, label = "* E3") +
theme_minimal()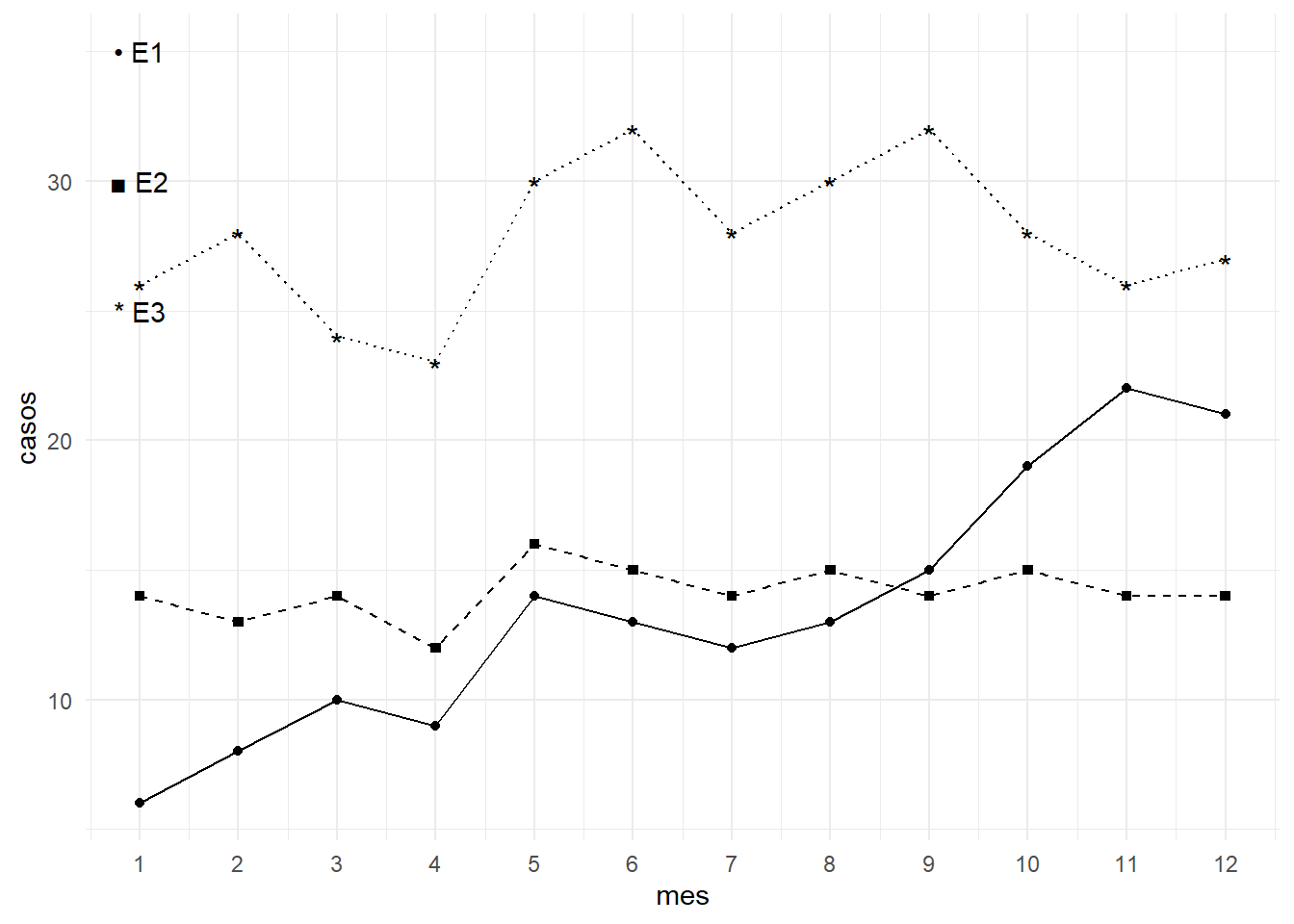
Dada la gráfica podemos observar que el escenario 3 es el peor de todos, y que el escenario 1 es el mejor dado que presenta menos casos que el resto en la mayoría de los meses. Sin embargo, esto puede llevarnos a errores ya que no estamos tomando en cuenta el canal endémico. Una mejor forma de comparar gráficamente los escenarios es sobreponiéndolos en la gráfica del canal endémico. Veámoslo.
canal_endemico_cisticercosis <- cisticercosis_guate |>
group_by(mes) |>
summarise(Li = quantile(casos, 0.25, type = 6),
Ie = quantile(casos, 0.5, type = 6),
Ls = quantile(casos, 0.75, type = 6)
)ggplot(canal_endemico_cisticercosis) +
geom_ribbon(aes(x = 1:12, xmin = 1,
ymin = 0, ymax = 36),
fill = "green") +
geom_ribbon(aes(x = 1:12, xmin = 1,
ymin = Li, ymax = 36), fill = "blue") +
geom_ribbon(aes(x = 1:12, xmin = 1,
ymin = Ie, ymax = 36), fill = "yellow") +
geom_ribbon(aes(x = 1:12, xmin = 1,
ymin = Ls, ymax = 36), fill = "red") +
geom_line(aes(e1$mes, e1$casos), linetype = 1) +
geom_point(aes(e1$mes, e1$casos)) +
geom_line(aes(e2$mes, e2$casos), linetype = 2 ) +
geom_point(aes(e2$mes, e2$casos), shape = 15) +
geom_line(aes(e3$mes, e3$casos), linetype = 3) +
geom_point(aes(e3$mes, e3$casos), shape = "*", size = 4) +
scale_x_continuous(breaks = seq(1, 12, 1)) +
scale_y_continuous(breaks = seq(0, 40 , 5)) +
xlab("Mes") + ylab("Casos") +
annotate(geom = "text", x = 2, y = 35, label = "• E1") +
annotate(geom = "text", x = 2, y = 33, label = "■ E2") +
annotate(geom = "text", x = 2, y = 31, label = "* E3") +
theme_classic()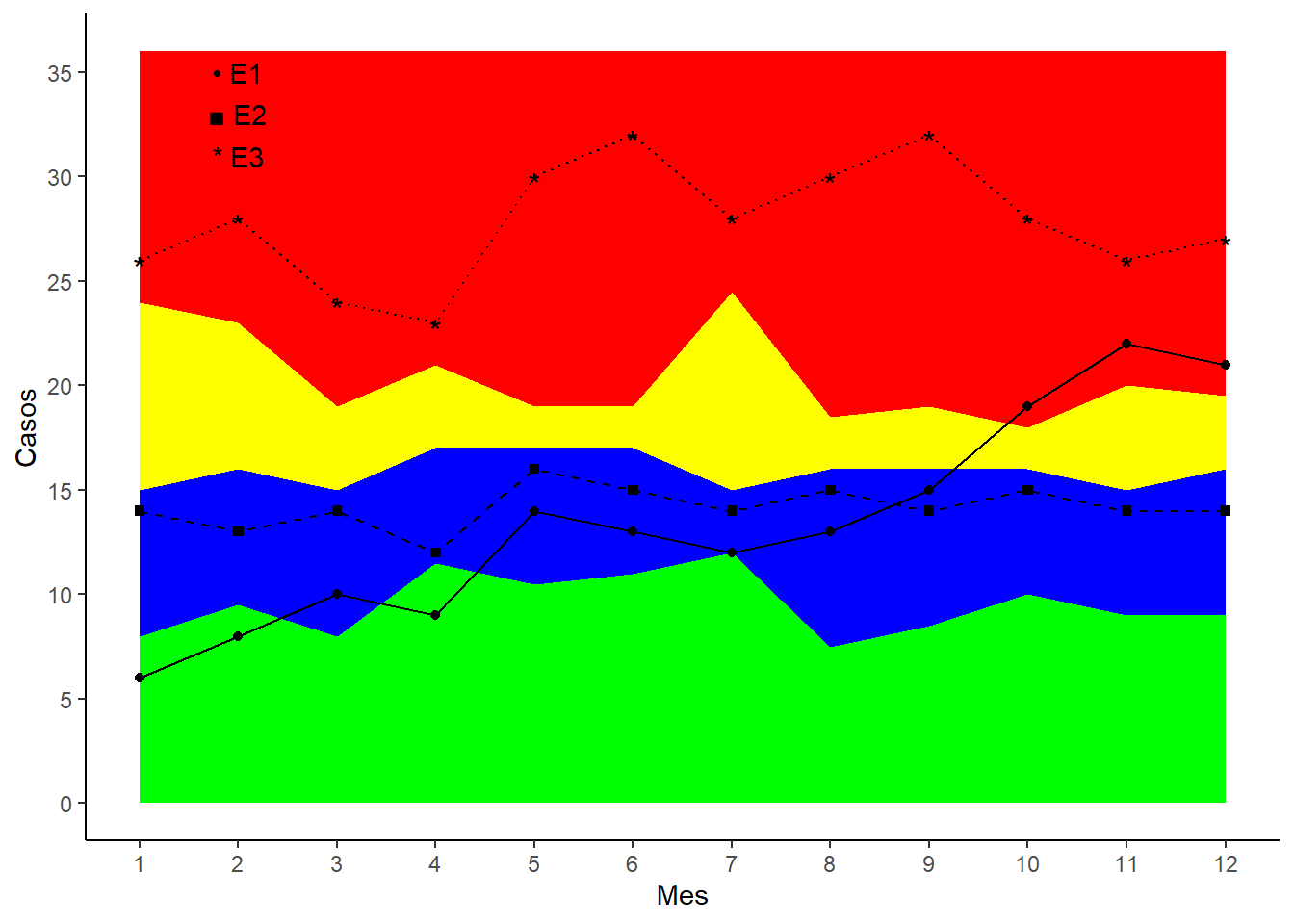
Con esta perspectiva queda más claro el panorama. El escenario 3 sigue presentándose como el peor de todos, pero ahora notamos que el escenario 1 que antes nos parecía mejor que el escenario 2 ahora nos parece peor ya que presenta 3 meses en el área endémica.
Otros factores importantes a tomar en cuenta: - El escenario 1 parece que sigue una tendencia a la alza, por tanto puede representar un riesgo mayor para los siguientes años. - El escenario 2 pese a tener la mayoría del año valores más altos que el escenario 1 se muestra más estable, por tanto es más probable que no escale.